Breadth First Search Shortest Reach

You will be given a number of queries. For each query, you will be given a list of edges describing an undirected graph. After you create a representation of the graph, you must determine and report the shortest distance to each of the other nodes from a given starting position using the breadth-first search algorithm (BFS). Return an array of distances from the start node in node number order. If a node is unreachable, return for that node.

Example
The following graph is based on the listed inputs:

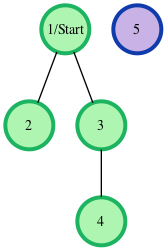
// number of nodes
// number of edges

// starting node

All distances are from the start node . Outputs are calculated for distances to nodes through : . Each edge is units, and the unreachable node has the required return distance of .

Function Description

Complete the bfs function in the editor below. If a node is unreachable, its distance is .

bfs has the following parameter(s):

int n: the number of nodes
int m: the number of edges
int edges[m][2]: start and end nodes for edges
int s: the node to start traversals from

Returns
int[n-1]: the distances to nodes in increasing node number order, not including the start node (-1 if a node is not reachable)

Input Format

The first line contains an integer , the number of queries. Each of the following sets of lines has the following format:

The first line contains two space-separated integers and , the number of nodes and edges in the graph.
Each line of the subsequent lines contains two space-separated integers, and , that describe an edge between nodes and .
The last line contains a single integer, , the node number to start from.

Constraints

Sample Input

Sample Output

6 6 -1
-1 6

Explanation

We perform the following two queries:

The given graph can be represented as:

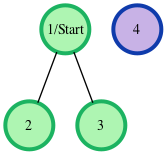
where our start node, , is node . The shortest distances from to the other nodes are one edge to node , one edge to node , and an infinite distance to node (which it is not connected to). We then return an array of distances from node to nodes , , and (respectively): .
The given graph can be represented as:

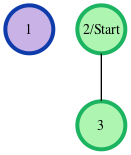
where our start node, , is node . There is only one edge here, so node is unreachable from node and node has one edge connecting it to node . We then return an array of distances from node to nodes.

Solution

#include <bits/stdc++.h>

using namespace std;

string ltrim(const string &);

string rtrim(const string &);

vector<string> split(const string &);

* Complete the 'bfs' function below.

* The function is expected to return an INTEGER_ARRAY.

* The function accepts following parameters:

* 1. INTEGER n

* 2. INTEGER m

* 3. 2D_INTEGER_ARRAY edges

* 4. INTEGER s

vector<int> bfs(int& n, int& m, vector<vector<int>>& edges, int& s)

{

map<int, list<int>> adj; // Create adjacent list

bool valid_test = false;

for (int i = 0; i < edges.size(); i++)

{

// Starting node validation (may not be connected)

if (edges[i][0] == s || edges[i][1] == s)

valid_test = true;

// Proceed with the lists

adj[edges[i][0]].emplace_back(edges[i][1]);

adj[edges[i][1]].emplace_back(edges[i][0]);

}

vector<bool> visited(n + 1, false); // All nodes

vector<bool> calculated(n + 1, false);

vector<int> distance(n + 1, 0); // Distances of all edges

vector<int> ans(n + 1, 0);

if (valid_test)

{

// BFS algorithm

queue<int> q; // The queue for the BFS algorithm

q.emplace(s); // Push the starting node first

while (!q.empty())

{

int current = q.front();

visited[current] = true;

q.pop();

// Traverse child nodes

for (list<int>::iterator itr = adj[current].begin(); itr != adj[current].end(); ++itr)

{

int child = *itr;

if (visited[child] == false && calculated[child] == false)

{

distance[child] = distance[current] + 6;

ans[child] = distance[child];

// Important: Nodes may share adjacent nodes

// Avoid re-calculating node distance

calculated[child] = true;

q.emplace(child);

}

vector<int>::iterator ans_itr = ans.begin();

ans.erase(ans_itr); // Remove the first position

for (int i = 0; i < ans.size(); i++)

{

// Erase the starting node

if (i == s - 1) ans.erase(ans_itr + s - 1);

if (ans[i] == 0) ans[i] = -1;

}

return ans;

}

int main()

{

ofstream fout(getenv("OUTPUT_PATH"));

string q_temp;

getline(cin, q_temp);

int q = stoi(ltrim(rtrim(q_temp)));

for (int q_itr = 0; q_itr < q; q_itr++)

{

string first_multiple_input_temp;

getline(cin, first_multiple_input_temp);

vector<string> first_multiple_input = split(rtrim(first_multiple_input_temp));

int n = stoi(first_multiple_input[0]);

int m = stoi(first_multiple_input[1]);

vector<vector<int>> edges(m);

for (int i = 0; i < m; i++)

{

edges[i].resize(2);

string edges_row_temp_temp;

getline(cin, edges_row_temp_temp);

vector<string> edges_row_temp = split(rtrim(edges_row_temp_temp));

for (int j = 0; j < 2; j++)

{

int edges_row_item = stoi(edges_row_temp[j]);

edges[i][j] = edges_row_item;

}

string s_temp;

getline(cin, s_temp);

int s = stoi(ltrim(rtrim(s_temp)));

vector<int> result = bfs(n, m, edges, s);

for (size_t i = 0; i < result.size(); i++)

{

fout << result[i];

if (i != result.size() - 1)

{

fout << " ";

}

fout << "\n";

}

fout.close();

return 0;

}

string ltrim(const string &str)

{

string s(str);

s.erase(

s.begin(),

find_if(s.begin(), s.end(), not1(ptr_fun<int, int>(isspace)))

);

return s;

}

string rtrim(const string &str)

{

string s(str);

s.erase(

find_if(s.rbegin(), s.rend(), not1(ptr_fun<int, int>(isspace))).base(),

s.end()

);

return s;

}

vector<string> split(const string &str)

{

vector<string> tokens;

string::size_type start = 0;

string::size_type end = 0;

while ((end = str.find(" ", start)) != string::npos)

{

tokens.push_back(str.substr(start, end - start));

start = end + 1;

}

tokens.push_back(str.substr(start));

return tokens;

}

Comments