Leetcode•Jul 02, 2025
Maximum Width of Binary Tree
Hazrat Ali
Leetcode
Given the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is guaranteed that the answer will in the range of a 32-bit signed integer.
Example 1:
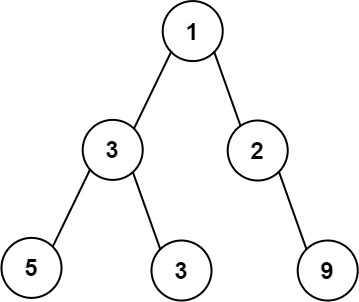
Input: root = [1,3,2,5,3,null,9] Output: 4 Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).
Example 2:
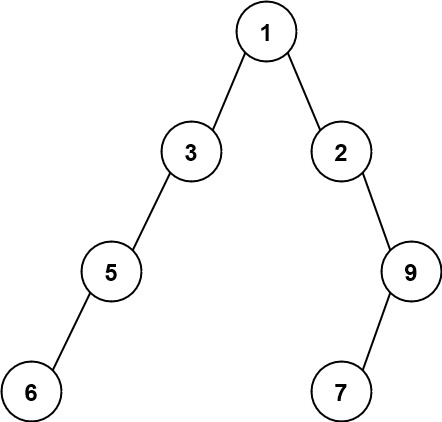
Input: root = [1,3,2,5,null,null,9,6,null,7] Output: 7 Explanation: The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
Example 3:
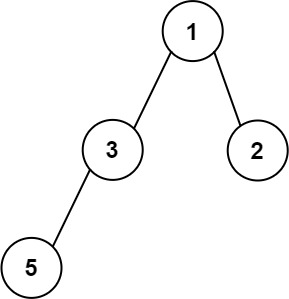
Input: root = [1,3,2,5] Output: 2 Explanation: The maximum width exists in the second level with length 2 (3,2).
Solution
/**
* @param {TreeNode} root
* @return {number}
*/
const widthOfBinaryTree = root => {
if (!root) {
return 0;
}
const q1 = [root];
const q2 = [0];
let max = 1;
while (q1.length > 0) {
const size = q1.length;
let left = 0;
let right = 0;
for (let i = 0; i < size; i++) {
const node = q1.shift();
const index = q2.shift();
if (i === 0) {
left = index;
}
if (i === size - 1) {
right = index;
}
if (node.left) {
q1.push(node.left);
q2.push(index * 2);
}
if (node.right) {
q1.push(node.right);
q2.push(index * 2 + 1);
}
}
max = Math.max(max, right - left + 1);
}
return max;
};