Codeforces•Oct 09, 2025

Bear and Friendship Condition

Hazrat Ali

Codeforces

There are n members, numbered 1 through n. m pairs of members are friends. Of course, a member can't be a friend with themselves.

Let A-B denote that members A and B are friends. Limak thinks that a network is reasonable if and only if the following condition is satisfied: For every three distinct members (X, Y, Z), if X-Y and Y-Z then also X-Z.

For example: if Alan and Bob are friends, and Bob and Ciri are friends, then Alan and Ciri should be friends as well.

Can you help Limak and check if the network is reasonable? Print "YES" or "NO" accordingly, without the quotes.

Input

The first line of the input contain two integers n and m (3 ≤ n ≤ 150 000, 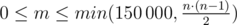) — the number of members and the number of pairs of members that are friends.

The i-th of the next m lines contains two distinct integers ai and bi (1 ≤ ai, bi ≤ n, ai ≠ bi). Members ai and bi are friends with each other. No pair of members will appear more than once in the input.

Output

If the given network is reasonable, print "YES" in a single line (without the quotes). Otherwise, print "NO" in a single line (without the quotes).

Examples
Input 
4 3
1 3
3 4
1 4
Output
YES
Input
4 4
3 1
2 3
3 4
1 2
Output
NO
Input
10 4
4 3
5 10
8 9
1 2
Output
YES
Input
3 2
1 2
2 3
Output
NO

Solution
#include <bits/stdc++.h>
using namespace std;

int n, m;
vector<vector<int>> g;
vector<int> color;

int dfs(int u) {
  color[u] = 1;
  int cnt = 1;
  for (auto v: g[u]) {
    if (color[v] == 0) {
      cnt += dfs(v);
    }
  }
  return cnt;
}

int main() {
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  cin >> n >> m;
  g.resize(n);
  color.resize(n);
  for (int i = 0; i < m; i++) {
    int u, v;
    cin >> u >> v;
    u--, v--;
    g[u].push_back(v);
    g[v].push_back(u);
  }
  bool ok = true;
  long long ec = 0;
  for (int u = 0; u < n; u++) {
    long long uc = dfs(u);
    ec += uc * (uc - 1) / 2;
  }
  if (ok and ec == m) {
    cout << "YES" << endl;
  } else {
    cout << "NO" << endl;
  }
  return 0;
}



Comments