Views Matter
Hazrat Ali
The height of the exhibit is equal to m. Consequently, the number of blocks in each stack is less than or equal to m.
There is a camera on the ceiling that sees the top view of the blocks and a camera on the right wall that sees the side view of the blocks.
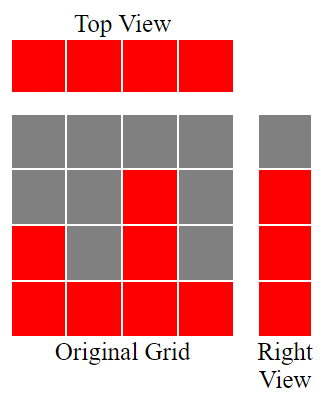
Find the maximum number of blocks you can remove such that the views for both the cameras would not change.
Note, that while originally all blocks are stacked on the floor, it is not required for them to stay connected to the floor after some blocks are removed. There is no gravity in the whole exhibition, so no block would fall down, even if the block underneath is removed. It is not allowed to move blocks by hand either.
The first line contains two integers n and m (1≤n≤100000, 1≤m≤109) — the number of stacks and the height of the exhibit.
The second line contains n integers a1,a2,…,an (1≤ai≤m) — the number of blocks in each stack from left to right.
Print exactly one integer — the maximum number of blocks that can be removed.
5 6
3 3 3 3 3
10
3 5
1 2 4
3
5 5
2 3 1 4 4
9
1 1000
548
0
3 3
3 1 1
1
Solution
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m;
cin >> n >> m;
vector<int> s(n);
long long sum = 0;
int mx = 1;
for (int i = 0; i < n; i++)
{
cin >> s[i];
sum += s[i];
mx = max(mx, s[i]);
}
sort(s.begin(), s.end());
int ans = sum - max(mx, n);
if (mx >= n and n > 1 and s[1] == 1)
{
ans--;
}
cout << ans << endl;
return 0;
}